In Reasoning Part, another important Topic is Inequality Problems. It is a common topic for all competitive exams. We can expect 5 or 6 questions from Inequality. It is one of the topic, where you can get full marks very easily. I am going to explain a very simple method and i assure you that it’s possible to solve 5 questions in just two minutes.
In Inequality, at first they give some directions for the Problems. And in each problem, there will be statements followed by 4 conclusions. Our job is to find the conclusions which are true.
There are two types of models in Inequality.
1) Coded Inequality.
2) Direct Inequality.
In Coded Inequality, symbols like $, #, %, &, @ are used. In Direct Inequality, we use symbols like <, >, =, ≤, and ≥ . Before learning shortcuts, lets understand what these symbols mean. Most of us learn these symbols in lower classes and they all are familiar ones.
< – Less than
≤ – Less than or Equal to
> – Greater than
≥ – Greater than or Equal to
= – Equal to
I hope everybody know this. Let’s go to Coded Inequality.
Directions
P $ Q means P is not smaller than Q
P @ Q means P is neither smaller than nor equal to Q
P # Q means P is neither greater than nor equal to Q
P ∂ Q means P is neither greater than nor smaller than Q
P © Q means P is not greater than Q
Now our first work is to find what does the symbol means indirectly?
Lets solve it one by one.
P is not smaller than Q. So P can be either equal to Q or Greater than Q. Symbol is ≥.
P is neither smaller than nor equal to Q. So P is Greater than Q. Symbol is >.
P is neither greater than nor equal to Q. So P is lesser than Q. Symbol is <.
P is neither greater than nor smaller than Q. So P is equal to Q. Symbol is =.
P is not greater than Q. So P can be either equal to or lesser than Q. Symbol is ≤.
Now form a small table before solving this kind of problems.
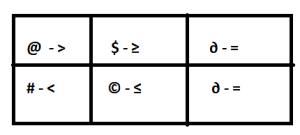
Now we decoded the symbols and we clearly know what is the meaning of each symbol. Make sure that you form a table as above. The symbols >, ≥, and = should be in one row and the symbols <, ≤, and = should be in another row. Don’t memorize the table. Usually Symbols change. You have to decode it correctly and form a table.
Note:
———-> Forward Direction.
<———- Reverse Direction.
In Row 1, First Priority should go to >. Next ≥. Last =. Similarly,
In Row 2, First Priority should go to <. Next ≤. Last =.
Just remember these lines. You will understand it while solving problems.
Never make a mistake in forming this table. If you make a mistake then you loose all the 5 or 6 marks.
We will try to solve some problems based on the above directions.
Example 1
Statements: N ∂ B, B $ W, W # H, H © M
Conclusions: (1) M @ W. (2) H @ N. (3) W ∂ N.

Step 1 – Make a single statement.
N ∂ B $ W # H © M
Step 2 – Analyze the conclusions one by one. Always compare with the Modified Statement.
1. M @ W
- If you draw a line from M to W, you will get a Reverse Line.
- Between M and W two symbols are there. One is © and other is #. Both are in row 2. Highest Priority is #. Since the letters form a reverse line, we should note the symbol which is exactly above #. The symbol above to # is @. So M @ W is TRUE.
2. H @ N
- If you draw a line from H to N, you will get a Reverse line.
- Between H and N, the symbols are #, $, and ∂.
- If you check these symbols with the table, # is in Row 2 and $ is in Row 1. So Conclusion 2 is FALSE.
3. W @ N
- If you draw a line from W to N, you will get a Reverse line.
- Between W and N, the symbols are $ and ∂. Between $ and ∂, the higher priority goes to $.
- The conclusion formed a reverse line. So we should note the symbol which is opposite to $. That is ©. But given conclusion is W @ N. So it is FALSE
So Conclusion one alone Follows
Example 2
Statements – R © D, D $ J, J # M, M @ K
Conclusions – 1. K # J. 2. D @ M 3. R # M. 4. D @ K
Step 1 – Modify the statement.
R © D $ J # M @ K
Table

Step – 2 – Analyze the conclusion one by one.
1. K # J
- Between K and J – Reverse Line. Symbols are – @ and #.
- In table @ and # are in different rows.
- Conclusion 1 – FALSE
2. D @ M
- Between D and M – Forward Line. Symbols are $ and #.
- In table $ and # are in different rows.
- Conclusion 2 – False.
3. R # M
- Forward line. Symbols are ©, $, and #.
- $ and # are in different rows.
- Conclusion 3 – False.
4. D @ K
- Forward Line. Symbols are $, # and @.
- Symbols are in different rows.
- Conclusion 4 – False.
NOTE: When more than one conclusion in false, check for merging concept. If the characters are same and both the statements are false, and while merging, if we get a meaningful symbol, then the statements can be merged. (To learn clearly about merging, check Syllogism Made Easy).
In the above problem, all the characters of the statements are different. So we can not merge it. So None is True.
Example 3
Statements: M $ K, K @ N, N © R, R # W
Conclusions: 1) W @ K 2) M $ R 3) K @ W 4) M @ N
Step 1: M $ K @ N © R # W

(You don’t need to draw table again and again. I am pasting it for your convenience.)
Analyzing Conclusions
1) W @ K – Reverse line. Symbols are #, ©, and @. In table # and @ are in different Rows. False.
2) M $ R – Forward Line. Symbols are $, @, ©. They are in different rows, False.
3) K @ W – Forward Line. Symbols are @, ©, #. They are in different rows, False.
4) M @ N – Forward line. Symbols are $ and @. Highest priority is for @. So M @ N is True.
Only Conclusion 4 is True.
Example 4
Statement: H @ T, T # F, F ∂ E, E © V.
Conclusions: 1) V $ F. 2) E @ T. 3) H @ V. 4) T # V

Modified Statement – H @ T # F ∂ E © V
Conclusions
1) V $ F – Reverse Line – Symbols are © and ∂. Both are in Row 2. Since it forms a reverse line, and highest priority is for ©, we should mark the symbol which is exactly opposite to ©. So the correct symbol is $. Conclusion 1 is True.
2) E @ T – Reverse Line. Symbols are ∂ and #. Both are in Row 2. High priority is #. Symbol opposite to # is @. So E @ T is True.
3) H @ V – Forward line. Symbols are in different rows. So False.
4) T # V – Forward line. Symbols are #, ∂, and ©. All are in Row 2. High Priority is for #. So T # V is True.
Answer – Conclusion 1, 2, and 4 are True.



